La géométrie avec Géogébra, ce n’est vraiment pas compliqué. Voici un exemple à travers un petit problème simple.

Dans un enclos, deux chèvres sont attachées chacune, par une corde, à un piquet différent. Le fermier ne dispose que d’une mangeoire. Il se demande où il pourrait la placer pour que ses deux chèvres puissent aller y manger en même temps. Pourriez-vous l’aider ?

Voici des informations.
Les deux piquets sont espacés de 16 carreaux.
La corde d’une des chèvres est longue de 9 carreaux et l’autre corde est longue de 10 carreaux.

Faire un croquis qui donne l’emplacement possible de la mangeoire.

Voici un problème de géométrie tout simple faisant intervenir les outils géométriques classiques: règle et compas.

En complément des activités de tracé manuel, toujours indispensables à l’école, nous vous proposons une approche numérique à l’aide du logiciel Géogébra.

Cette approche peut être envisagée de deux manières; la façon la plus classique sera, sans doute, de privilégier la recherche à l’aide des outils classiques et d’aborder le numérique en complément. Une autre approche consiste à privilégier d’abord l’approche numérique, puis à utiliser les outils pour effectuer les mesures et la construction.

Les deux approches sont complémentaires.

Que ce soit avec le numérique ou avec les outils classiques, une fois le problème résolu, on peut aller plus loin. Faire varier les données de l’énoncé (l’espacement entre les piquets, la longueur des cordes) pour créer un problème analogue,  aborder de nouvelles questions (existe-t-il une condition sur la longueur des cordes ?) , ou complexifier le problème: que se passe-t-il si notre fermier possède 3 chèvres placées en triangle ? Comment situer la troisième chèvre par rapport aux deux autres ?

On se rend compte, si on décide d’aller plus loin, de la plus-value des outils numériques. Rien de plus simple, en effet, que de dessiner quelques cercles, de les agrandir ou de les rétrécir, de les déplacer avec Géogébra… Ce qui est difficile avec les outils classiques.

En combinant les deux outils, vous permettrez à vos élèves d’aborder la géométrie sous deux angles complémentaires: la manipulation des outils pour la construction des figures et la manipulation dynamique des objets sur le plan euclidien.

Utiliser Géogébra

Il existe une version en ligne de ce logiciel, que nous allons exploiter ici. Il suffit donc d’un navigateur récent et d’une connexion à Internet.

Géogébra en langue française, c’est ici: https://www.geogebra.org/?lang=fr

Pour accéder aux outils géométriques, rendez-vous tout en bas de la page d’accueil, et cliquez sur le lien « géométrie ». Ou cliquez directement ici :

https://www.geogebra.org/geometry

On démarre sur une page blanche avec quelques outils.

Première étape: placer le quadrillage

Cliquer sur « Propriétés », en haut à droite (bouton 1) 

Choisir « afficher grille – quadrillage complet. Il est possible d’ajuster le quadrillage à l’aide des outils « loupe » (2), ou en utilisant la molette de la souris.

Deuxième étape: poser les deux piquets

On pourrait matérialiser les deux piquets par deux points ou par un segment (3) dont les extrémités sont séparées par 16 carreaux. Mais on peut aussi, directement, positionner les cercles matérialisant la distance maximale aux piquets. On peut, bien sûr, donner des directives aux élèves en ce sens mais cela irait à l’encontre de notre travail de recherche. Indiquons-leur quels sont les éléments qu’ils ont le droit d’utiliser : le point, le segment, le cercle, ainsi que les outils « effacer » et « déplacer », et laissons-les trouver eux-mêmes une méthode. On pourra toujours discuter, lors de la mise en commun, de la méthode la plus efficace.

Pour effacer

Pour effacer les points, utiliser l’icône « effacer », dans le menu « édition ».

Pour accéder au menu « édition », cliquer sur « PLUS ».

Cliquer sur l’icône « effacer » puis sur le / les éléments à effacer.

Pour modifier ou déplacer

Cliquer sur l’icône « déplacer », en forme de flèche. Cette icône permet ensuite de déplacer ou de modifier n’importe quelle figure.

Il n’est pas nécessaire de  situer correctement les figures lors de la phase de tracé. En effet, pour déterminer le rayon d’un cercle, il peut être plus simple de positionner le centre à l’intersection d’une ligne et une colonne principales, et ensuite, de déplacer la figure en cliquant sur le contour. C’est un des avantages du numérique sur le papier !

Voici notre croquis final, sur une approche « minimale » (donc sans point additionnel, sans segment).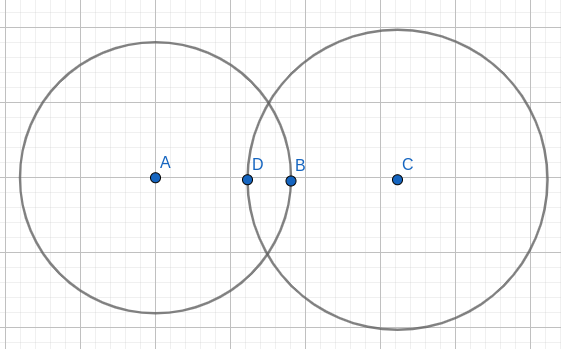

Il est maintenant possible d’aller plus loin. Par exemple, demander quelle est la distance maximale entre les deux piquets pour que l’on puisse placer une mangeoire ? Voilà encore un avantage du numérique sur le réel: il suffit de déplacer l’un des deux cercles pour obtenir la réponse.

Enregistrer le travail

Dans Géogébra, on peut enregistrer le travail pour le reprendre ultérieurement. Il n’est pas nécessaire de créer un compte.

Cliquez sur le menu(4) puis sur « sauvegarder ». Donner un nom à la sauvegarde. Celle-ci sera stockée sur l’ordinateur. Pour la récupérer ultérieurement, allez dans le menu « Fichier »- « ouvrir ». Là, à droite, choisir l’icône « dossier » pour parcourir l’ordinateur. Trouver le fichier et valider.

Une fois le travail terminé, on peut aussi l’exporter sous divers formats, dont le pdf. Toujours dans le menu « Fichier ».